再帰関数を使ってフラクタル図形を描く
この記事は後編です。
前編をまだお読みでない方は下記URLから読んでいただくとすんなりと理解いただけると思います。
さて後編の今回では実際にscratchでフラクタル図形を描いていきたいと思います。いくつかフラクタル図形の描き方を紹介しつつ、再帰関数の利用方法についても少し考察していきます。
それではいってみましょう！
実際に描いてみよう
フラクタル図形が描かれる様子は見ていてとても楽しいです。ぜひ皆さんもScratchを開き一緒にプログラムを作って実行してみてください。プログラムの説明については多少複雑なところがありますが頑張って理解してみてください。再帰関数など使いこなせればプログラミングでできることの幅が大きく広がりますよ！
シェルピンスキーのギャスケット
三角形の組み合わせでできたフラクタル構造を持つ図形です。
シェルピンスキーのギャスケットを描くためのプログラムは以下の通りです。
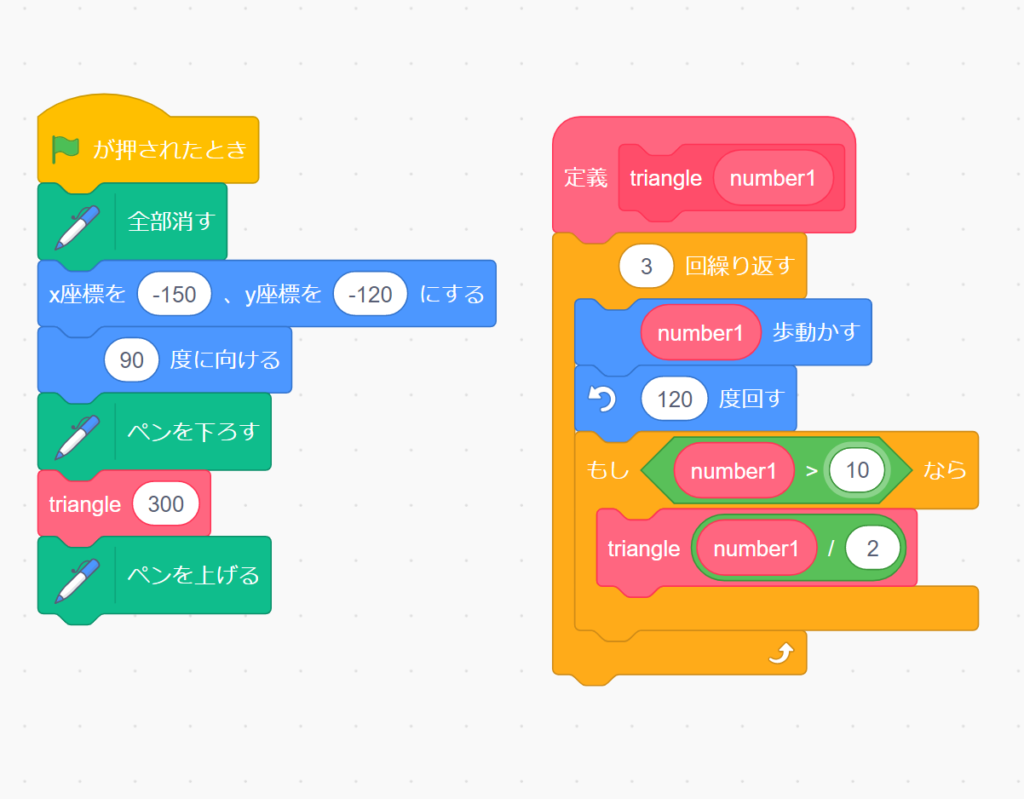
ペンを扱うブロックについては馴染みがない人も多いと思うので簡単に説明しておきますね。
全部消す ： 画面にあるペンで描かれた線を全部消す
ペンを下ろす ： ペンを上げるまでスプライトの軌跡が線になる
ペンを上げる ： ペンを下すまで線が描かれないようになる
といった具合ですね。結構直感的に操作できるのでなれれば簡単です。それでは緑旗が押されたときから順番に見てみましょう。プロジェクトがスタートしたらまず画面にある線をすべて消します。その後スプライトを指定の場所に持っていきます。今回は図形の左下からスタートして一辺が300の大きさにする予定なのでだいたいx座標が-150、y座標が-120と設定するとよいでしょう。
スプライトが指定の場所についたらスプライトの向きを90度にします。この向きが線を描く方向になります。そうやってスプライトの初期設定が出来たらペンを下ろし、再帰関数であるtriangleを引数300で実行、その後ペンを上げてプログラムを終了する。これがこのプログラムの流れです。
詳しいtriangle関数の説明は再帰関数内の条件文”もしnumber1>10”の10を80にして考えます。そうすると次の画像のようにシェルピンスキーのギャスケットが少しわかりやすくなります。
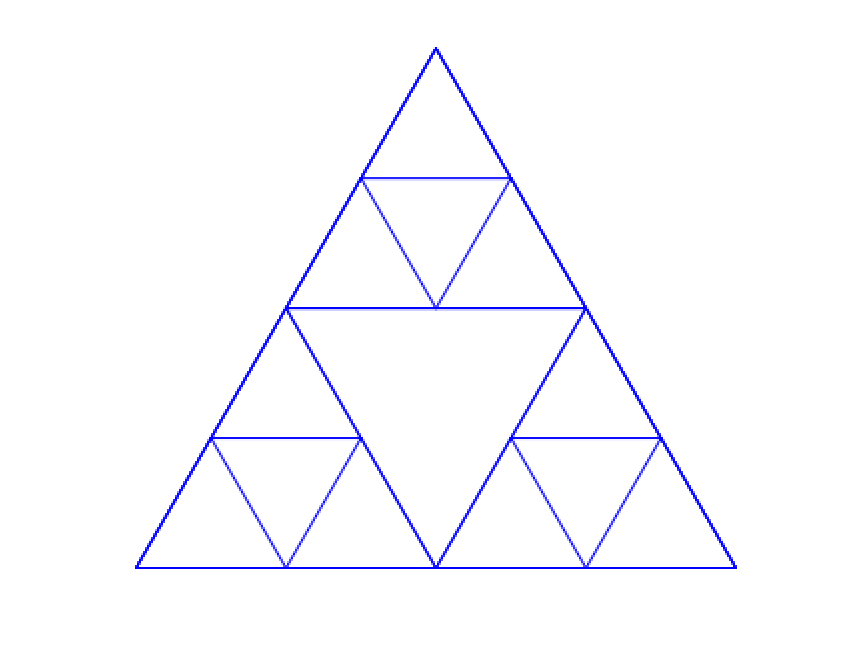
triangle関数内で行っていることは最大の三角形の一辺を描き、その後120度（正三角形の角度）スプライトを回転させ現在の半分の長さの一辺を描く。これを一辺の長さが80より小さくなるまで続けています。ちなみに300÷2=150,150÷2=75ですから辺の長さが違う三角形を三種類描くことになります。（条件が80以上の場合）
そして辺の長さが最小の三角形を描き終わったら2番目に短い三角形のもう一辺を描き、その後また最小の三角形を描くことになります。そうやって3度繰り返したらもう一段階長い三角形のもう一辺を描き……というふうにしてシェルピンスキーのギャスケットを描いています。
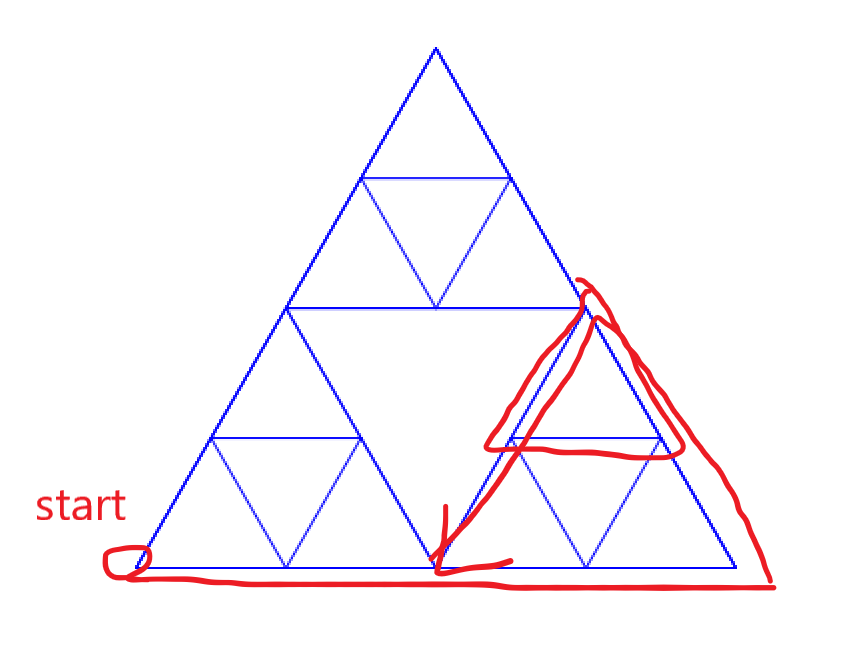
コッホ曲線
コッホ曲線とは線分を三等分し、分割した2点を頂点とする正三角形の作図を無限に行うことでできる図形です。折り紙を折って山を作る感じですかね……このコードはシェルピンスキーのギャスケットよりも複雑です。できるところまででいいので自力で仕組みを理解してみるととても勉強になりますよ！
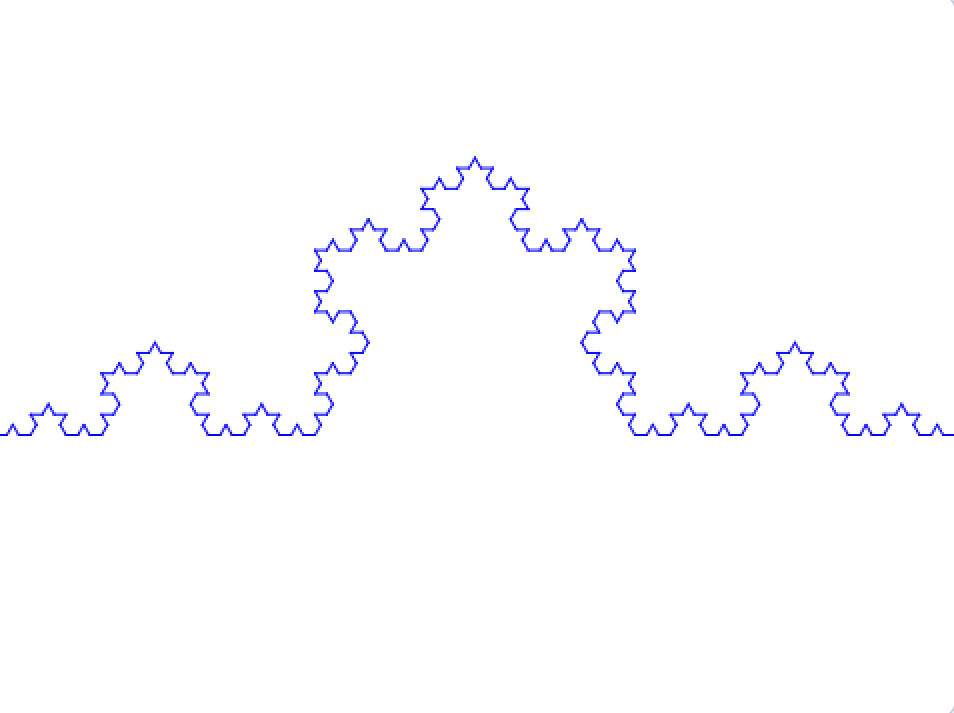
実際のコード
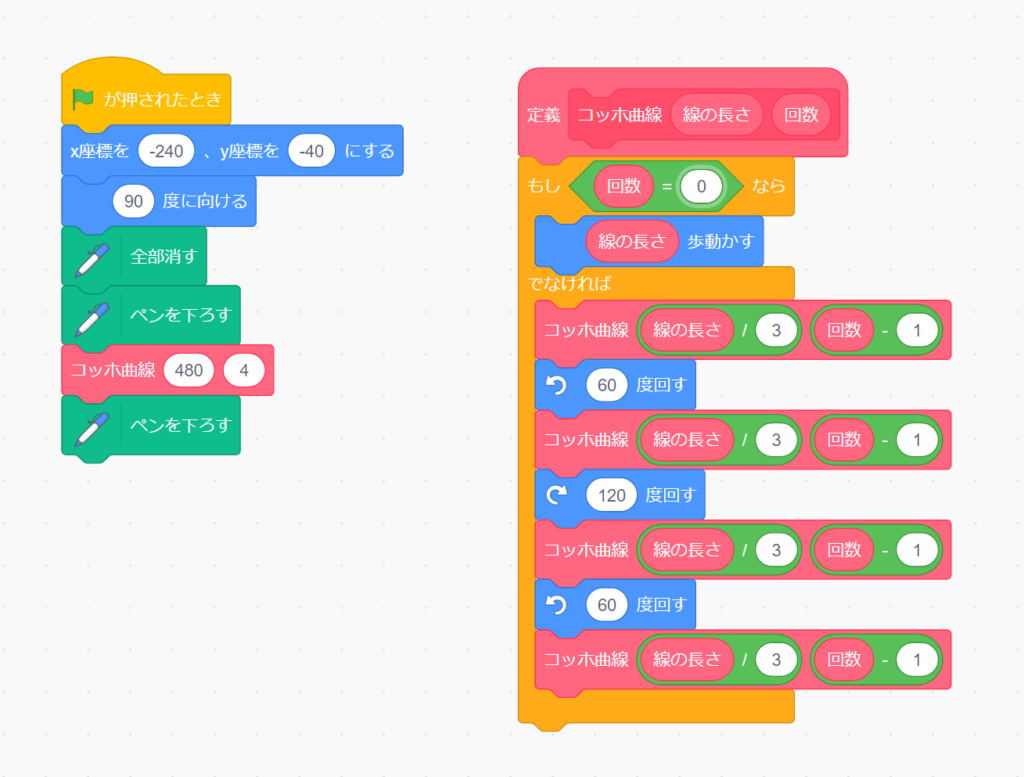
最後に
前編後編2回にわたって勉強したScratchでフラクタル図形を描く方法はいかがでしたか？一見複雑そうな図形も再帰関数をうまく使うことで簡単に描けてしまえます。フラクタル図形を描く以外にも再帰関数は様々なところで使われています。例えば再帰関数をうまく利用することで目的地に着くための経路を求める問題であったり複雑な数学の問題などもあっさり解けてしまったりするのです。これは”探索”というプログラミング特有の要素が関わっていたりするのですがこのお話はまたの機会に。
それではここまで読んでいただきありがとうございました！
Leave a Comment